THEME 3: ENABLING ALGORITHMS

The last thirty years have seen massive progress in the technical means of collecting data, through sensors, mobile phones, satellites, the internet and digitised administrative records. This has resulted in exponential increases in the amount of data that has been collected and could potentially be collected. Such data abundance creates the obvious challenges of storage, management, processing, analysis, visualisation, communication and utilisation. However, it also creates some important, yet subtle challenges arising out of the nature of the datasets. For example, a dataset may have missing data that would be important for its analysis, or there could be only sparse observations on some of the data attributes or subgroups of interest. We observe this, for example, in the data collected about the recent serious bushfires and in COVID19 data.

Enabling Algorithms provide the tools to carry out important computational tasks for a wide range of practitioners who need to understand the information that can be derived from datasets and models. For example, the algorithms can be used to extract useful information through data summarization, model fitting, and model prediction. ACEMS members working on this theme improve current best practice and develop new methodologies to solve a range of problems. Solutions involve multiple approaches such as optimisation, simulation and mathematical approximation. Such solutions need to be robust and stable; they should also be principled in the sense that it can be shown mathematically that they perform as claimed under a wide range of conditions. Achieving such algorithmic performance requires drawing from the wide spectrum of mathematical, statistical, machine learning and computational capabilities within the Centre.

The Enabling Algorithms developed by ACEMS are used by international researchers, and by members of the other themes in ACEMS: Challenging Data, Multiscale Models and Informed Decisions. Conversely, and most importantly, input from the other themes in ACEMS informs the research of the Enabling Algorithm group.

People

Key Achievements

In 2019, ACEMS researchers worked to improve existing methods and to develop new methodologies to solve a range of problems. Some of these achievements are described below.

The University of Technology Sydney node hosted the 2019 Enabling Algorithms Theme symposium on 13th-14th June 2019 on the topic of fast approximate inference. Professor David Nott (National University of Singapore) was the keynote speaker. The symposium featured talks from nine other speakers and tutorials on fast approximate inference methodology. ACEMS post-doctoral research fellow Dr Wilson Chen spent the last year of his post-doctoral fellowship working on Stein point Markov chain Monte Carlo methodology and semiparametric generalised autoregressive conditional heteroscadasticity models. The Stein point Markov Chain Monte Carlo research involved collaboration with Professors Mark Girolami and Chris Oates at the Alan Turing Institute in the United Kingdom. Professor Oates was an ACEMS post-doctoral fellow during 2015-2017.

Jointly with Zdravko Botev (UNSW), Joe Grotowski (UQ), CI Dirk Kroese was awarded the 2019 Gavin Brown Prize by the Australian Mathematical Society for their paper Kernel density estimation via diffusion, which appeared in The Annals of Statistics. They presented a new adaptive kernel density estimator based on linear diffusion processes. The proposed estimator builds on existing ideas for adaptive smoothing by incorporating information from a pilot density estimate. In addition, they proposed a new plug-in bandwidth selection method that is free from the arbitrary normal reference rules used by existing methods. They presented simulation examples in which the proposed approach outperforms existing methods in terms of accuracy and reliability.

Cover image of Data Science and Machine Learning: Mathematical and Statistical Methods.

ACEMS researchers CI Dirk Kroese and AIs Thomas Taimre and Slava Vaismann (also with Zdravko Botev from UNSW) published their book Data Science and Machine Learning: Mathematical and Statistical Methods, Chapman and Hall/CRC, 2019. This book provides an accessible, yet comprehensive textbook intended for students interested in gaining a better understanding of the mathematics and statistics that underpin the rich variety of ideas and machine learning algorithms in data science. It focuses on mathematical understanding, the presentation is self-contained, accessible, and comprehensive and it also includes an extensive list of exercises and worked-out examples. New Python software for Data Science and Machine Learning was also made available on GitHub.

PhD student Rixon Crane and AI Fred Roosta developed a new algorithm DINGO for distributed Newton-type optimization of gradient norms in learning networks. This algorithm optimizes a large sum of functions in a distributed computing environment, using a novel communication-efficient Newton-type algorithm that enjoys a variety of advantages over similar existing methods. The algorithm was published in the prestigious NeurIPS conference.

CI Peter Forrester was involved in a chance project with Santosh Kumar (Shiv Nadar University, India) on a computer algebra assisted recursive algorithm to compute the distribution of the largest eigenvalue for (real and complex) Wishart matrices, which is of interest in multivariate statistics as a test of a certain null hypothesis, as well as in theoretical physics in quantifying bipartite entanglement in a random setting, among other applications. The paper has been published.

A common approach to modelling real-world systems is to describe the observations through a statistical likelihood. For many systems, however, it is either very difficult or not possible to write down a tractable formula for this likelihood. This has motivated research into approximate likelihoods. ACEMS AI Chris Drovandi and CI Kerrie Mengersen collaborated on a prestigious book chapter that reviews two approaches for estimating the intractable likelihood, with the goal of reducing the necessary model simulations to produce an approximate posterior. The first of these is a Bayesian version of the synthetic likelihood, which uses a normal approximation to the summary statistic likelihood. The second is based on constructing an empirical likelihood, which involves maximising a likelihood constructed empirically under a set of moment constraints. The latter can be constructed in a Bayesian framework to completely avoid model simulations in some cases. These approaches were illustrated on models of varying complexity.

AI Chris Drovandi’s Bayesian synthetic likelihood (BSL) research progressed significantly in 2019. BSL is a scalable Monte Carlo method for likelihood-free inference problems (thus it fits in both Monte Carlo algorithms and tailored algorithms). Journal articles were published in Statistics and Computing and Journal of Computational and Graphical Statistics by his ACEMS PhD student Ziwen An. These articles aimed to increase the robustness and computationally efficiency of BSL.

In 2019 AI Chris Drovandi also made progress on his project on sequential Monte Carlo (SMC) methods. An article was published in Bayesian Analysis by completed ACEMS PhD student Leah South (now at Lancaster University, UK). The paper was in collaboration with CI Tony Petitt. In 2019 a new ACEMS PhD student Josh Bon started research on SMC methods. This project will be in collaboration with Dr Anthony Lee (Bristol University, UK), and potentially other researchers from the UK.

ACEMS PhD student Matthew Sutton, with ACEMS co-authors Benoit Liquet and Kerrie Mengersen, found flaws in current deflation methods and proposed a new sparse Partial Least Squares (PLS) method wherein the direction vectors are constrained to be sparse and lie in a chosen subspace. The proposed technique has been shown to outperform alternative sparse PLS techniques for coefficient estimation. Moreover, a simple renormalisation step can be used to improve the estimation of sparse PLS direction vectors generated using any convex relation method.

CI Ian Turner and AI Professor Liu and research collaborators from China continued their work on the development of efficient computational algorithms for solving fractional space and/or time partial differential equations. Their PhD student Libo Feng completed his PhD thesis research and graduated from QUT in July.

CI Turner, AI Liu and collaborators undertook important work concerning novel parameter estimation techniques for fractional dynamical epidemic models published in Numerical Algorithms. In that work an inverse problem was considered to identify the parameters for a fractional-order differential system that modelled an outbreak of dengue fever using data from the 2009 outbreak of the disease in the Cape Verde islands. They proposed a numerical method for the fractional-order dengue fever system based on the Gorenflo-Mainardi-Moretti-Paradisi scheme solved using the Newton method. The modified grid approximation method and the modified hybrid Nelder-Mead simplex search and particle swarm optimization algorithms were used to estimate the model parameters. The modified hybrid scheme was found to be the most effective and efficient of the parameter estimation strategies investigated. In particular, the multi-term fractional-order dengue fever system provided the best fit to the data with the lowest root-mean-square error.

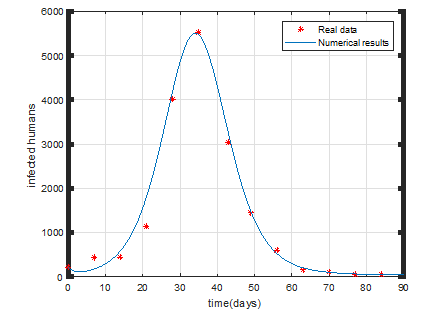
Number of infected humans in the 2009 Cape Verde outbreak computed using the multi-term fractional model versus the measured data.

CI Turner and AI Professor Hegland from the ANU developed methods for approximating functions of covariance or precision matrices of Gaussian processes. They derived a new approach that uses Chebyshev polynomials and a Moebius transform which maps the spectrum of the precision matrix onto the interval (0, 1). They used Python, Chebfun and spatial indexing based on a kd-tree from Scipy's spatial algorithms and data structures package to generate large and sparse precision matrices. AI Hegland presented this work at the 2019 AustMS annual meeting during the session on computational mathematics.

CIs Turner, Burrage and Wand are collaborating on the use of univariate quadrature methods for approximating Integrals arising in computational statistics. They have considered Gauss-Hermite quadrature, transformed Gauss-Legendre quadrature and transformed Gauss–Kronrod quadrature techniques. This research work is ongoing.

CI Turner, AI Farrell and postdoctoral fellow Steve Psaltis continued their work with the Queensland Government Department of Agriculture and Fisheries on developing models to predict the modulus of elasticity (MOE) of logs from core measurements extracted from standing trees. Strong correlations between estimated and measured log MOE were obtained. The study revealed that a single core from the breast height of a tree allows a good prediction of the log MOE. The slope of the regression line of the predicted versus measured values was close to unity, highlighting the robustness and minimum bias of the model. A cross validation using a bootstrap resampling technique was used to demonstrate the strong correlation.

They also extended their previous studies of property variation in the southern pines resource by developing wood property models of sawn timber boards. These properties can be used to predict the value of the resource, and are therefore of critical importance to the forestry industry.

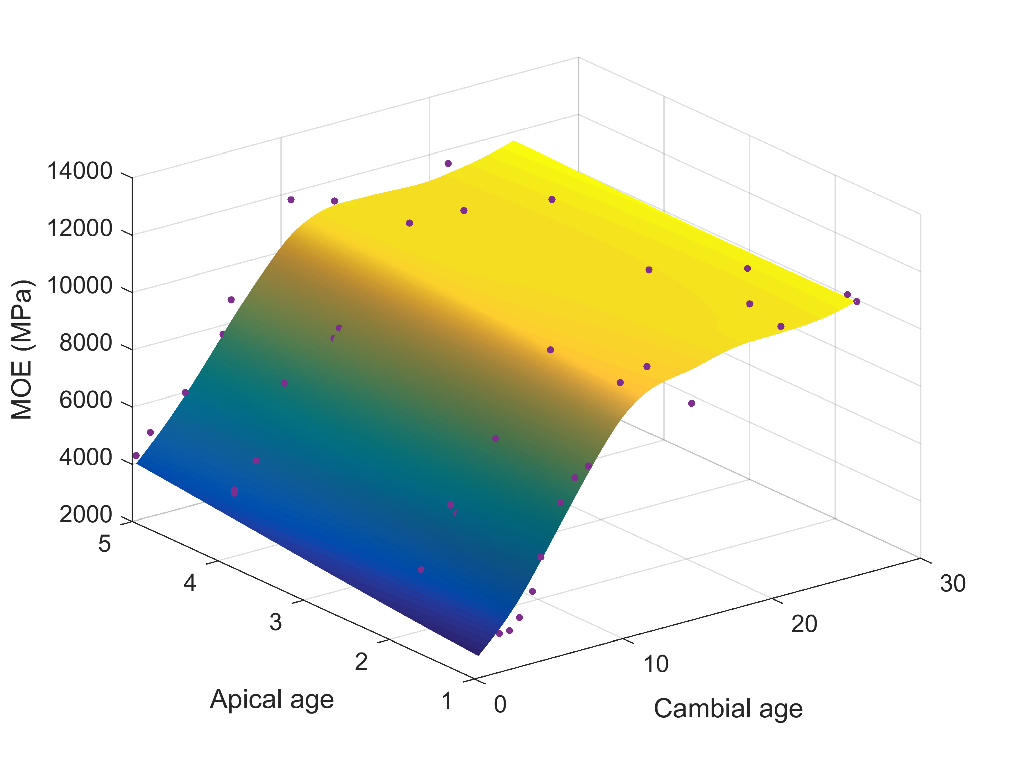
Representative radial basis function surface fitted to the measured data.

By utilising industrial sawing patterns, they are able to virtually saw the modelled logs to extract the boards, together with their associated properties, and then compare predicted values with those measured on the sawn boards. They found that the models gave moderate correlation to the measured MOE values.

ACEMS Research Fellow Steve Psaltis has continued working with Richard Taylor in the School of Electrical Engineering and Robotics at QUT. He is developing mathematical models describing the dynamics of vortices that occur in type-II superconductors. Taylor and his group are developing experimental methods to measure and visualise vortices in superconducting samples, and this will be used as validation of the models. This work is part of two grants with Defence Materials Technology Centre (DMTC) and Defence Science and Technology Group (DST Group).

Vortices within a Type-II Superconductor, with a square shaped defect located in the centre. The defect has different material properties and hence exhibits different vortex dynamics.

Research Fellow Psaltis undertook an ACEMS International Mobility Program visit to the Mathematical Institute at the University of Oxford, hosted by Prof Colin Please, where they worked on developing reduced-order models of lithium-ion batteries. They used the mathematical method of multiple-scales homogenisation to systematically derive reduced-order macroscopic models of diffusive behaviour in materials which have microscopic structure consisting of large rapid variations in conductivity. The research is motivated by the need to develop a simplified model that describes the electrical and thermal behaviour of lithium-ion cells and accounts for effects due to the macroscale geometry of highly conductive metallic current collectors and poorly conductive electrodes. They exploit the vast differences in length scale within a typical cell, namely the length of the current collectors and the small distances between current collectors. Furthermore, they consider various distinguished limits of the electrical and thermal conductivities of the various elements of the cell. This work is ongoing through regular Skype meetings, and a paper is currently in development.

CI Turner and Research Fellow Psaltis commenced a new project with the Department of Agriculture and Fisheries, investigating the impact of continuous drying on key production and performance criteria of engineered wood structural elements. The main aim of this work is to extend existing two-dimensional computational code that models the vacuum and conventional drying of Australian hardwoods to incorporate three-dimensional simulation capabilities of the continuous drying process. Psaltis investigated three-dimensional meshing procedures involving both triangular prisms and tetrahedra. Once the calculation of the three-dimensional mesh properties was verified, work commenced on converting the computational parts of the code to three dimensions. A considerable number of changes were required to convert the two-dimensional model to three dimensions. A three-dimensional linear diffusion problem with constant, isotropic diffusivity, prescribed constant flux on the boundaries and constant initial conditions was used as a benchmark problem. Given this constant flux, the variation of the average value in the domain over time can be determined analytically. They found that the analytical and numerical results are in excellent agreement, giving confidence in our implementation of the three-dimensional model. This research work is ongoing.

Plans for 2020

Plans for 2020 are already well underway, and the following is a brief summary of what ACEMS researchers working across Australia in the Enabling Algorithms Theme are planning to do:

• Develop efficient Monte Carlo methods for deep learning networks.
• Create novel second-order optimisation techniques for machine learning networks.
• Expand the theoretical foundations and efficacy of Monte Carlo sampling algorithms such as Hamiltonian Monte Carlo.
• Work on sparse structures in ensemble neural networks.
• Design new simulation algorithms for spatial point processes.
• Work on Monte Carlo methods for decision making.
• Develop algorithms for empirical mode decomposition.
• Derive approximate maximum likelihood estimators for generalized linear mixed models based on Thouless-Anderson-Palmer approximation methods.
• Work on anomaly detection and high dimensional time series.
• Improve variational approximations for intractable likelihood approximations for both time series and random effects models.
• Develop Nonparametric copula models.
• Improve ABC and synthetic likelihood methods to intractable likelihood models.
• Improve particle methods for Dynamic Stochastic General Equilibrium models in macroeconomics.
• Improve methods for Symbolic Data Analysis.
• Develop computation and inferential schemes for extreme value modelling.
• Create novel algorithms and model representations for partitioning processes.
• Improve techniques for modelling with neural networks.