THEME 2: MULTISCALE MODELS

Nature works on multiple scales. Water is more than individual molecules; the economy is more than individual agents. Multiscale Models reflect the fundamental mathematical and statistical structures required to understand the relationships between the behaviour of systems when they are studied at different levels of focus. The research teams within this theme are working to develop new models and mathematical techniques, both stochastic and statistical in nature, to understand these highly complex problems.

Such an objective requires ACEMS researchers working in very different fields of mathematics and statistics to come together, share their challenges and determine how they can each benefit the other. At one end of the spectrum are the applied statisticians who develop useful insights about how appropriate modelling strategies need to change, in order to adapt to the granularity of data measurements from the real world. At the other end are the theoretical mathematicians who use abstract and deep results in pure mathematics to shed light on concepts such as the theory of polynomials in many variables, and provide advanced tools to facilitate computational algorithms. And while these two seemingly widely divergent fields appear poles apart, it is the work of the applied probabilists, the mathematical physicists, the theoretical statisticians, and those mathematicians and statisticians that fall at different points of the spectrum, that brings the abstract to the real world, creating a pipeline of opportunity for new applications and discoveries.

As a result, the Multiscale Models theme research is some of the most diverse within ACEMS, ranging all the way from theoretical mathematics to applied statistics and machine learning.

People

Key Achievements

In 2019 research groups across ACEMS worked to understand and develop models that account for structure at various hierarchical levels.

The University of Queensland node made several notable contributions to the field of stochastic processes in 2019. In collaboration with Research Fellows McVinish and Hodgkinson, CI Pollett studied distributional approximations for a general class of models called occupancy processes. These processes encompass stochastic patch occupancy models in ecology, network models in epidemiology, and a variety of dynamic random graph models. Bounds on the rate of convergence to a normal approximation were obtained using Stein’s Method, and the group was able to identify a subclass of weakly interacting processes exhibiting approximately Gaussian behaviour. The group also developed a significant extension of the “tau-leaping” method, for performing fast simulation of models in chemistry. When combined with fast summation methods, their method offers considerable improvement in speed over the standard Doob-Gillespie algorithm.

In another biological modelling paper, CI Taylor collaborated with University of Melbourne colleagues Jennifer Flegg and James McCaw, Monash colleague Mark Flegg and The University of Melbourne undergraduate student Somya Mehra to extend a model of White et al for how malaria hypnozoites develop in the human liver. This work was accepted by the Bulletin of Mathematical Biology, an exceptional achievement for an undergraduate student such as Somya.

In a cross-node collaboration between The University of Queensland and The University of Melbourne, ACEMS researchers made significant progress in understanding the growth of tissue in a developing organism. Specifically, CIs Pollett and Taylor, together with AI Tafakori, succeeded in deriving continuum models by scaling discrete agent-based models for cell proliferation.

In another cross-node collaboration, between CI Bean (UoA) and AI O’Reilly (UTas), the pair developed the first analysis of the Yaglom limit of stochastic fluid models. Bean and O’Reilly also collaborated with AI Nguyen (UoA) to develop a discontinuous Galerkin method for approximating the stationary distribution of stochastic fluid-fluid processes. This provides the first computational method enabling practical analysis of such processes. In addition, Bean and Nguyen developed a stochastic fluid model of the coral bleaching process. Finally, together with PhD student Angus Lewis (UoA), Bean and Nguyen also made significant advances in the estimation of Markovian-regime-switching models with independent regimes, motivated attempts to accurately model electricity spot price.

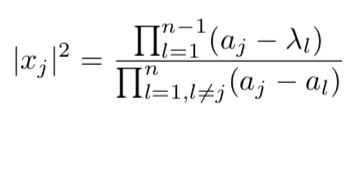
Formula discovered by CI Forrester and PhD student Jiyuan Zhang, cited in the Quanta article.

A group at The University of Melbourne, led by CI Forrester, made a number of advances in random matrix theory in 2019. PhD student Anas Rahman made important discoveries concerning asymptotic expansions in the matrix size. PhD student Allan Trinh analysed spectrum edge regimes, and the transition between them. In all cases considered, there is a choice of centring and scaling that leads to a fast rate of convergence. A study of the spectrum singularity universality class from this viewpoint is being undertaken in collaboration with ACEMS postdoc Shi-Hao Li. ACEMS Research Fellow Jesper Ipsen has been studying random matrix products and their applications to multiplicative processes. Contributions have also been made by PhD student Jiyuan Zhang, and a formula he and Forrester discovered has attracted attention in the popular science publication Quanta: www.quantamagazine.org/neutrinos-lead-to-unexpected-discovery-in-basic-math-20191113/.

During 2019, CI de Gier (UoM) continued work with PhD student Zeying Chen on an extended paper following upon their Physical Review Letters publication from 2018. With Research Fellow Xin Zhang, de Gier elucidated spectral details for a two-species integrable stochastic process with open boundaries. This result is the first of its kind for a model with boundary reservoirs. With Research Fellow Garbali, de Gier investigated a 2+1 dimensional statistical mechanical model based on the gl(1) toroidal algebra. The ultimate goal is to design a 2+1 dimensional stochastic process for which a precise mathematical analysis of universality is feasible. In related work, AI Michael Wheeler has continued his influential research program in integrable probability with collaborators at MIT, on the interplay between the theory of multi-variable polynomials and stochastic processes.

In collaboration with Youjin Deng from the University of Science and Technology of China, a team from the Monash node, consisting of CI Garoni, Research Fellow Zhou and PhD student Abrahim Nasrawi, published the first systematic study of the self-avoiding walk on the complete graph. This model describes how self-avoiding walks behave when confined to a finite box with periodic boundary conditions, when the number of spatial dimensions becomes large. Combined with the group’s work on the Random-Length Random Walk model from 2018, this now provides a quantitative universal understanding of the effect of periodic boundaries on statistical mechanical models in high dimensions.

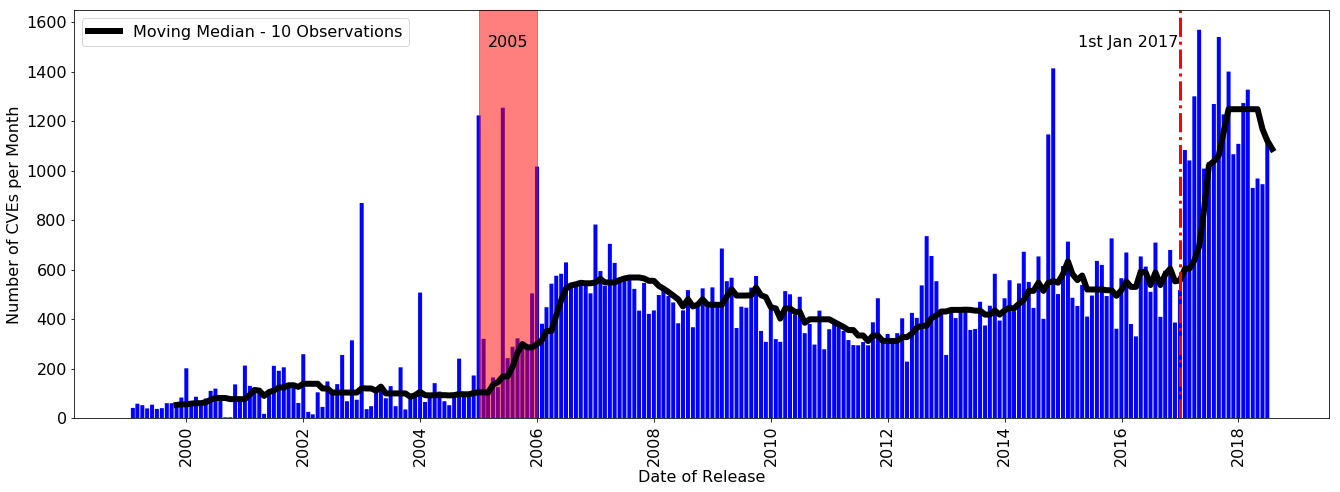
Time series of CVE arrivals.

The Common Vulnerabilities and Exposures (CVE) database is an important repository for information on cybersecurity vulnerabilities. More vulnerabilities get added every day, which creates an ongoing workload for those who have to manage cybersecurity. A group at The University of Adelaide, led by CI Roughan and AI Ross, in collaboration with Data61 member and PhD student Andrew Feutrill, have been working to enhance people's ability to manage cybersecurity. They have shown that the CVE workload arrival process is self-similar: it exhibits variability at every time scale, indicating an underlying complex system. However, they have also shown that a very simple change in the way this workload is ordered can significantly decrease the typical processing time of a CVE entry.

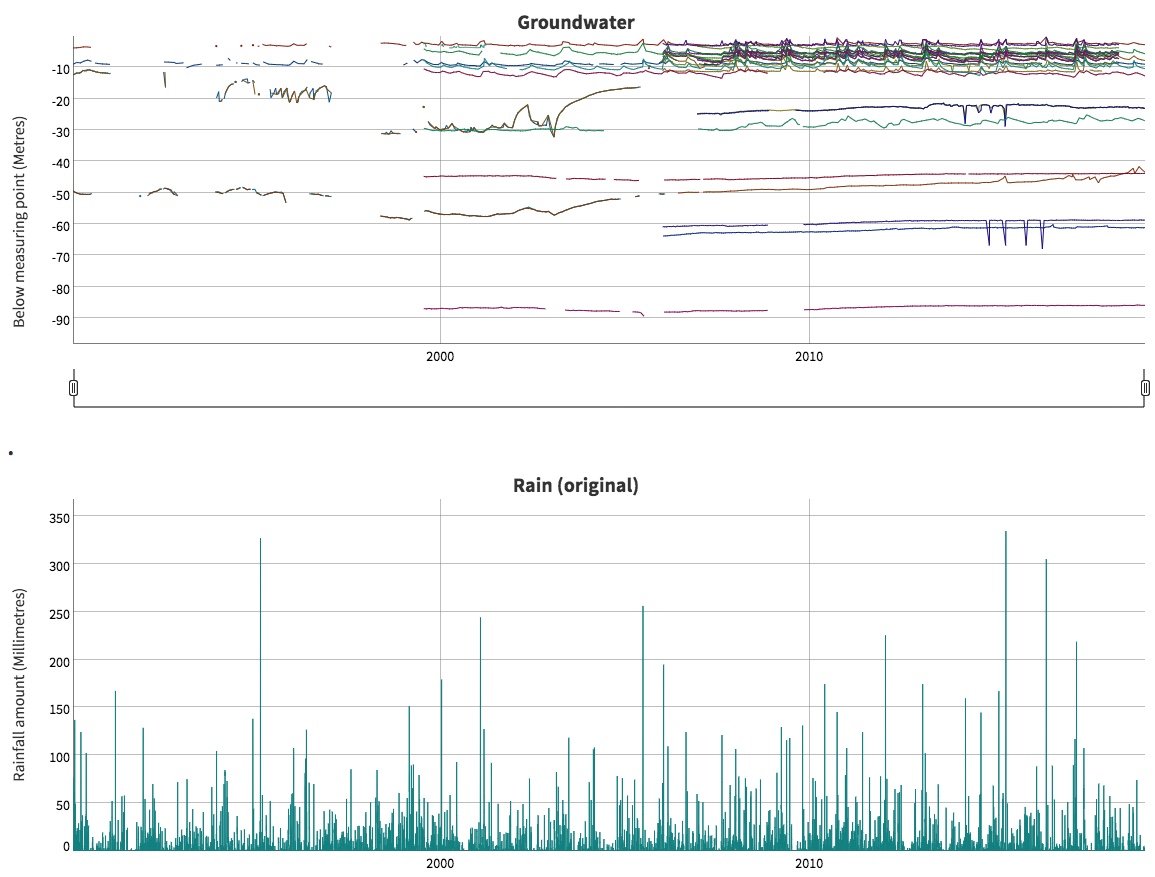
Screenshot of a hydrograph produced by Ryan, Hyndman and O'Hara-Wild.

During 2019, CI Ryan (UTS) engaged with the NSW Office of the Chief Scientist and Engineer, advising them on decision making under uncertainty. One specific project involved a collaboration with the Monash node, specifically CI Rob Hyndman and student Mitchell O'Hara-Wild, looking at levels of various groundwater bores in north eastern NSW. The researchers created an RShiny interactive tool that can be used by stakeholders to explore how the levels change over time and also how they respond to rainfall. The project also raised many interesting questions for future research.

In joint work on genetic risk for osteoporosis, CIs Ryan and Wand (UTS), with Research Fellow Toczydlowska and Tuan V. Nguyen of the Garvin Institute, investigated the association between genetic information of patients and their tendency to the loss of bone mineral density (BMD). The team examined different characterisations of the components which influence the loss of BMD. Assuming that the loss of BMD varies stochastically around its population curve over age, the team proposed a family multilevel linear mixed models that includes individual and cohort components to investigate a stochastic long-term trend in the level of BMD. One innovative aspect of the project is that the team predicted the rate of change of BMD, not BMD itself.

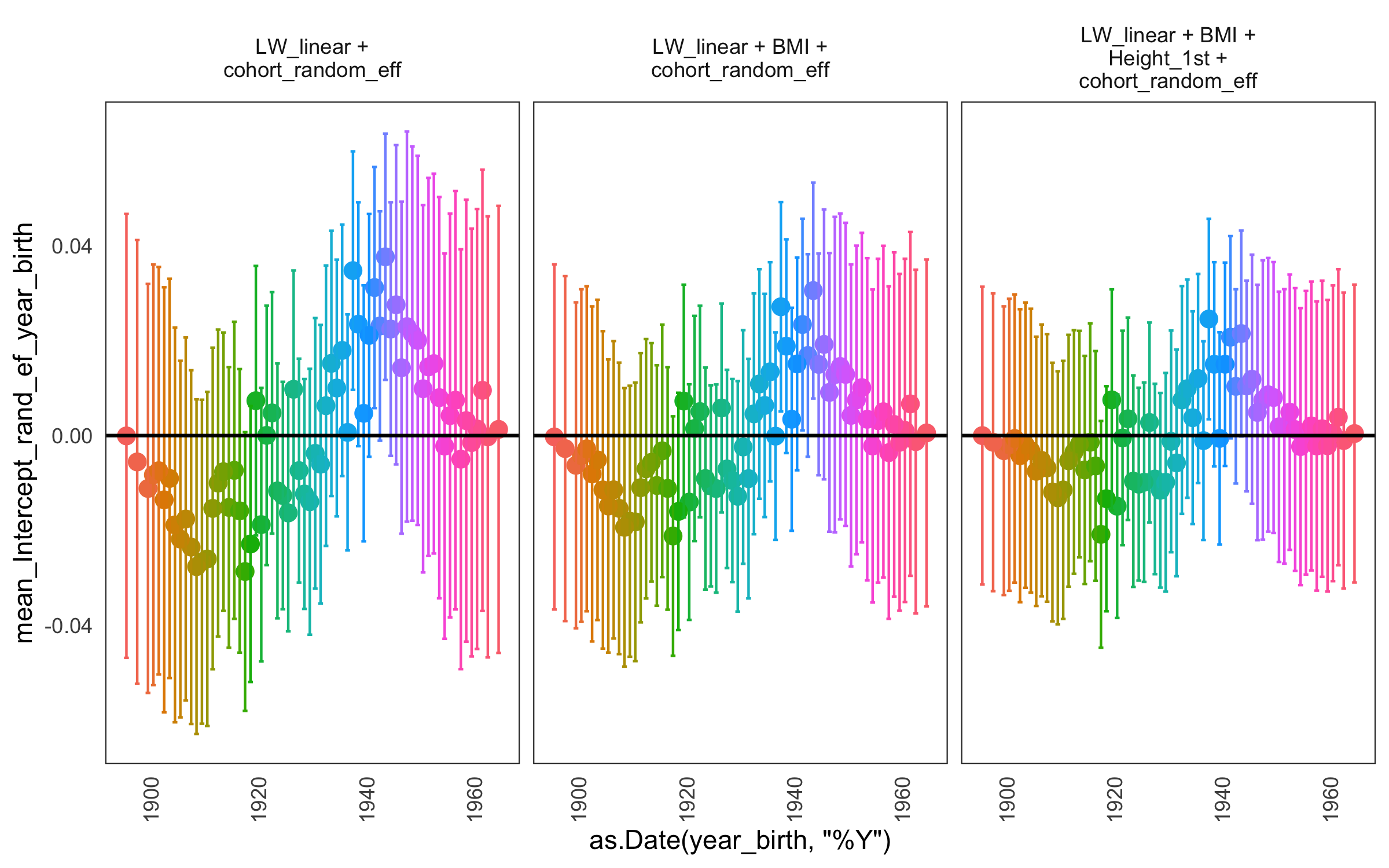
The random intercept corresponding to the year of birth effect in various examined models.

A classic example of the use of a multiscale modelling approach occurred in the work of CI Taylor, AIs Bowden and Keeler and South African colleague Krzesinski in their analysis of the block arrival data observed in the Bitcoin blockchain since the chain started in 2009. Viewed at a local timescale of days or weeks, a reasonable approximation to the block-mining process is that it is a Poisson process with a constant rate that is slightly faster than the design rate of six blocks per hour. However, this doesn’t take into account longer-term changes in the mining effort (which is called the `hashrate’) and the consequent change in the difficulty level of the cryptographic problem whose solution lies at the heart of the blockchain protocol. Based on blockchain block arrival data, the team presented a framework for studying the block arrival process at two levels: combining a local model for a period of constant difficulty with a long term model of how the difficulty changes over time.

CI Taylor, AI Bowden and colleague Krzesinski have also been developing a model to study a separate aspect of blockchain technology, revolving around varying the ratio of the expected block propagation delay to the expected mining interval. Current blockchains generally operate with this ratio kept very low, with the result that the mining community is usually in consensus about the state of the blockchain. Not surprisingly if this ratio is raised it is much more difficult for a blockchain to achieve absolute consensus. However, an exciting result of the research is that it still occurs with respect to all apart from a few outer nodes of what is now a blocktree rather than a blockchain.

CI Taylor’s work on fluctuation identities of Markov additive processes with his international colleagues Jevgenijs Ivanovs from Denmark and Guy Latouche from Belgium has continued. It is very close to completion, with a major paper due to be submitted in 2020.

Plans for 2020

Plans for 2020 are already well underway, and the following is a brief summary of some of what ACEMS researchers across Australia are planning to do:

• Relate the study of optimal finite size corrections to the longest increasing subsequence problem from the theory of stochastic combinatorial models in the KPZ universality class. It still remains to catalogue finite size corrections in all the classical ensembles, these being the cases for which analytic formulas are most readily available, so facilitating asymptotic analysis. Such systematic studies will be undertaken. (Forrester)
• Study various measures of aggregation used in parasitology. (Pollett)
• Study metapopulation models where there is no fixed ceiling on the number of habitat patches that can be occupied. (Pollett)
• Extend the work to develop more sophisticated predictive models for bore water levels, as a function of rainfall, temperature, ocean surface temperature and other predictors. (Ryan)
• Develop theory and algorithms for determining optimal designs in multilevel models with non-Gaussian response data. (Wand)
• Develop new statistical methodology for model selection in generalized additive mixed model contexts. (Wand)
• Finalise the collaboration with Garvan Institute in Sydney on genetic risk for osteoporosis. (Wand and Ryan)
• Publish extended versions of our 2018 Physical Review Letters article, with full mathematical proofs of the stated asymptotics for the random-length random walk. (Garoni)
• Publish an extended version of our 2018 Physical Review Letters article on multispecies exclusion processes. (de Gier)
• Extend the blocktree model for a block generating system with a large relative propagation delay. (Taylor)
• Complete the fluctuation theory of general Markov Additive processes. (Taylor)
• Look at healthcare and other applications of scheduled queueing models. (Taylor)
• Investigate spatial queueing models. (Taylor)