
CASE STUDY
Powerful new techniques and results for tackling complex occupancy process models
PEOPLE
An outbreak of a virus never seen before starts in one part of the world. Will it spread or just die out? If it does spread, how far?
This is an example of an epidemiology problem that a mathematician might try to model using what is known as an occupancy process. Other examples of occupancy processes include patch occupancy models used in ecology that might predict the extinction of a species over time, or random graph models used to study social and computer networks.
Occupancy processes are of great interest to ACEMS researchers at The University of Queensland (UQ).
“We treat real-world complex systems as a large collection of interacting sites. In the case of a virus, think of the sites as being countries or regions within those countries, with a site being ‘occupied’ if the virus is present in that region,” says Professor Phil Pollett, an ACEMS Chief Investigator at UQ.
“Clearly the virus can spread, not just from neighbouring sites, but from geographically distant sites because of air travel.”
At any particular point in time, the sites will be in a specific 'state'. Most models of practical interest run into problems when the number of potential states becomes prohibitively large. In this virus example, the total number of potential states at each timepoint depends on the number n of sites. Since each site can be in one of two states -- occupied or not occupied – there are 2n states.
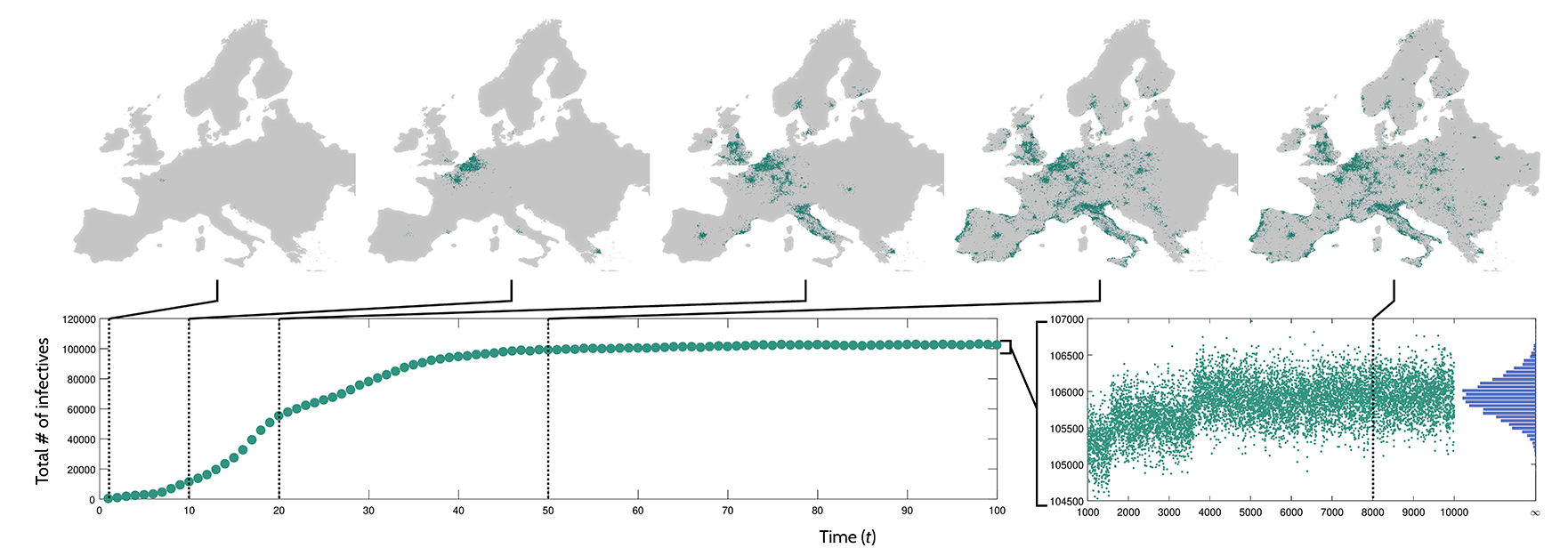
Figure 1: This figure illustrates the simulation of a complex model of a large-scale epidemic in Europe. The five maps depict the spread of the infection at five timepoints, while the graphs below show how the total number of infectives increases over time, including at the five timepoints. Notice how, despite the complexity of the model, the trend of infectives appears almost smooth and deterministic (non-random) on the macroscopic scale (as shown in the left graph), but, on a finer scale (the right graph) the fluctuations appear to follow a normal distribution (the blue bell-shaped curve). The ACEMS team formalised these observations into useful approximations. These new techniques and results apply to all models under the ‘occupancy process umbrella’ which is a major achievement.
"Liam brings to the project energy and enthusiasm, and a deep knowledge of Stein’s method and moment inequalities. These probabilistic methods have not been used previously in the present context, and were the key to providing the breakthrough we sought," says Phil.
Add to that the issue of what Phil calls geographical long-range dependence.
“Unlike models predominant in physics, such as the famous Ising Model, which account only for nearest neighbour interaction, the state at any particular site can be affected by the state at any of the sites or, indeed, all of them,” says Phil.
To tackle this challenge, Phil teamed up with one of his PhD students, Liam Hodgkinson, and ACEMS Associate Investigator Ross McVinish. They created a modelling framework that encompasses many models studied previously in these different fields. Their solution involves both an analytical method and a computational (simulation) method.
The team's analytical method deals with identifying approximating models. These are different kinds of models that are much easier to analyse, and which provide very good approximations for quantities of interest.
Phil says, though, it is not just a matter of ‘A approximates B’.
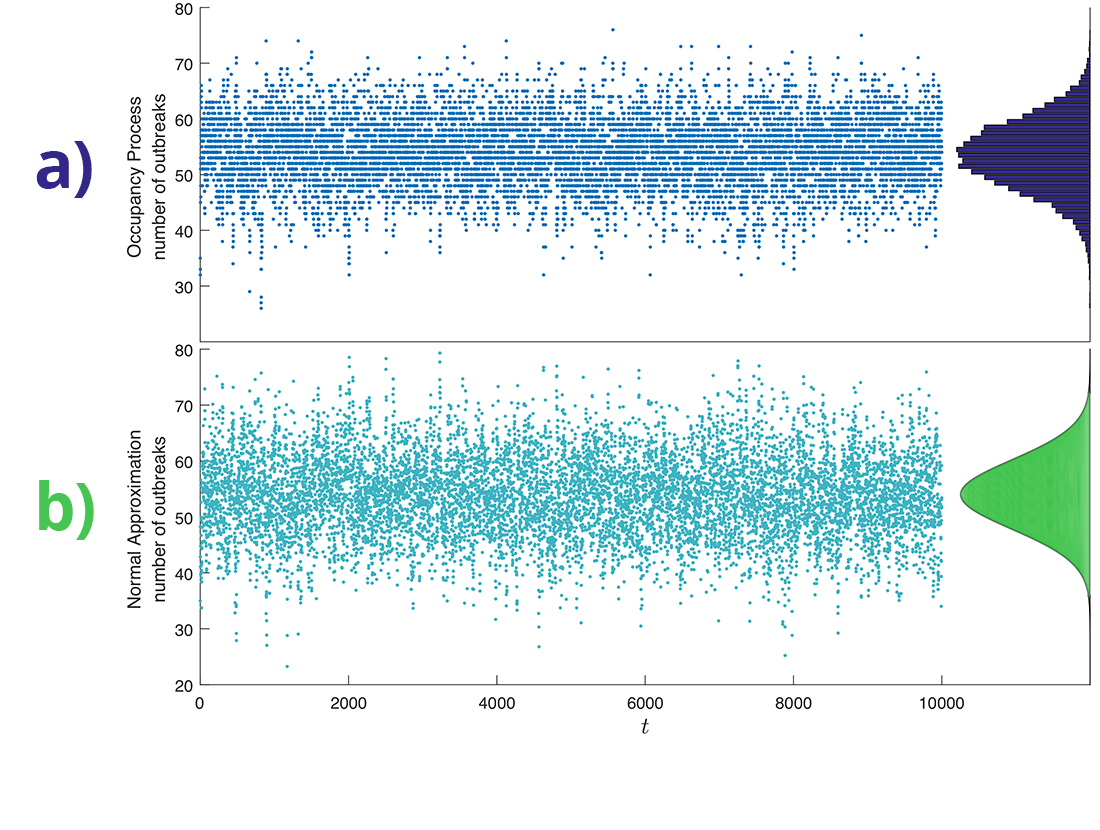
Figure 2: Simulation of (a) an epidemic process in equilibrium, together with its empirical distribution, and (b) the approximating model.
“Our methods say much more. They allow us to identify the most appropriate approximating model, and to be very precise about the size of the error in our approximations, even to the extent of saying under what conditions the approximation will be good,” says Phil.
The computational method involves another kind of challenge.
“The problem here is not so much recording and updating the state of the system, which we already know can be very large. Rather, it is that times between transitions are very short, and the transition rates, which govern the evolution of the process, need to be updated after each transition,” says Phil.
The team proposed a new algorithm for the approximate simulation of occupancy. The basic idea is to decouple sites over small time intervals so that the process is treated as a collection of independent two-state processes (one for each site). The transition rates are not fixed, but the resulting system is comparatively simple. The sites are recoupled and the transition rates updated, and then the sites are decoupled again, and so forth.
“It still seems unbelievable to me that it works, because your simulation is unfaithful to the model over short periods. But it does work, and Liam and Ross have provided detailed analytical results which prove that it does,” says Phil.
Consequently, the team’s analytical and computational methods can handle a wide range of models used by researchers around the world to study many different problems and issues.
“We have developed new techniques and results that apply to all models under the ‘occupancy process umbrella’,” says Phil.
And that is a breakthrough worth celebrating.